
2018 EMS-EWM Summer School
by Luz Roncal and Diana Stan
Nonlocal interactions in Partial Differential Equations and Geometry
Institut Mittag-Leffler, 21 – 25th May 2018, Stockholm, Sweden




Organisers. Luz Roncal and Diana Stan (Basque Center for Applied Mathematics – BCAM)
School webpages:
Abstract
European Women in Mathematics Summer Schools are intended to provide a stimulating intellectual environment for PhD students and post-docs from different countries and various mathematical disciplines, with special encouragement for the participation of women mathematicians. In April 2017, the European Women in Mathematics (EWM) and European Mathematical Society (EMS) opened a call for proposals for the organisation of the 8th Summer School in a series initiated by EWM.
For this 8th edition -held at the Institut Mittag-Leffler (IML) in Spring 2018- the selected proposal concerned Nonlocal Interactions in Partial Differential Equations and Geometry. The topics of the Summer School were embedded in the area of Elliptic Partial Differential Equations and they had a strong motivation from Geometrical Analysis.
The Summer School was mainly aimed at PhD students and post-docs interested in deepening their understanding of these topics and, as explained above, female mathematicians were especially encouraged to participate.
The theory of second-order elliptic equations has been flourishing during the last fifty years, making some substantial advances during the last years. Deep mathematical concepts lead to the field of Elliptic PDE’s, such as competitive systems, scattering theory or the Yamabe problem. The frameworks of study may be also diverse, ranging from the Euclidean setting to hyperbolic spaces. Moreover, there are important applications to population dynamics, theoretical physics or differential geometry. In Europe, there is an important mathematical community working in the area of Elliptic PDE’s, in particular, brilliant women mathematicians with strong influence in the development of the field.
The main goal of this Summer School was to introduce two research lines of current interest in Elliptic PDE’s: Competitive Interaction Systems and The Fractional Yamabe Problem. These topics were developed through the corresponding series of lectures. The titles of the mini-courses and the lecturers were:
- Geometric Aspects of Phase Separation lectured by Prof. Susanna Terracini from the University of Torino, Italy.
- The Fractional Yamabe Problem, lectured by Prof. María del Mar González from the University Autónoma of Madrid, Spain.
Both Prof. María del Mar González and Prof. Susanna Terracini are outstanding researchers in the area of Partial Differential Equations. They are world-recognized experts in their fields, and their lectures were certainly stimulating.
The lectures were complemented with plenary talks, long and short talks and a poster session. In this way, PhD students, post-docs and young researchers had the opportunity to be actively involved in the School.

Oversight Committee
The Oversight Committee was appointed by EWM and the EMS Women in Mathematics Committee in consultation with IML. It consisted of
- Ulrike Tillmann (Oxford University) — Chair
- Camilla Hollanti (Aalto University)
- Angela Pistoia (Sapienza Università di Roma)
- Sandra Pott (Lund University)
- Sandra di Rocco (KTH Royal Institute of Technology)
- Donna Testerman (École Polytechnique Fédérale de Lausanne)
Organising Committee
- Luz Roncal (Basque Center for Applied Mathematics, Spain)
- Diana Stan (Basque Center for Applied Mathematics, Spain)
Appointed Administrator at the IML
- Jenny Wiklund
Participants
The workshop had a total of 34 participants, including the two organisers, of which
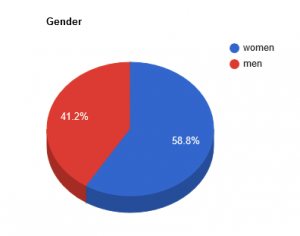
- Gender: 20 women, 14 men.

- Academic status: among the participants there were 5 postdocs, 13 PhD students and 1 master student.
- Nationalities: 11 Spanish, 9 Italian, 4 Romanian, 1 Indian, 1 Norwegian, 1 Austrian, 1 German, 1 Korean, 1 Swedish, 1 Brazilian, 1 Polish, 1 Turkish, 1 Russian.

Structure of the School
One of the aims of the School was to give all the participants the possibility to get involved in the School’s activities by presenting their research, either with a talk or a poster. This led to a very stimulating environment, because the presentations naturally lead to questions and discussions.
The schedule included 2 mini-courses (5 hours each), 5 plenary talks given by experts in the field, 6 talks by postdocs (30 minutes each) and short talks by PhD students and early career postdocs. A poster session was also organised. The structure was as follows:
- 2 mini-courses of 5 hours each: Susanna Terracini and María del Mar González.
- 5 plenary talks given by: Begoña Barrios (Universidad de la Laguna, Spain), Veronica Felli (Università di Milano Bicocca), Monica Musso (Bath UK and Santiago de Chile), Sundaram Thangavelu (Indian Institute of Science of Bangalore, India), Mariana Smit Vega Garcia (University of Washington)
- 6 long talks: Jørgen Endal (NTNU Trondheim, Norway), María Medina (Santiago de Chile), Lucilla Corrias (Université Val D’Evry), Cristina Brändle (University Carlos III Madrid), Eleonora Cinti (University of Bologna), Katrin Grunert (NTNU Trondheim, Norway).
- 10 short talks of PhD students and early career postdocs: Elisa Afilli, Judith Berendsen, Andreea Grecu, Miłosz Krupski, Azahara DelaTorre, Nikita Simonov, Denisa Stancu-Dumitru, Daniel Eceizabarrena, Javier Martínez, Havva Yoldas.
- Poster session: Maria Farcaseanu and Sangdon Jin.
The Summer School was developed in a very friendly and easygoing atmosphere. This fact encouraged the participants to be part of the School’s progress in many ways: by asking questions at the end of the talks, by taking part in blackboards discussions, and by motivating group or individual work.
Financial Support
| Quantity | Institution |
|---|---|
| 2000 euro | European Women in Mathematics |
| 2000 euro | European Mathematical Society |
| 800 euro | Basque Center For Applied Mathematics |
The funding was devoted to:
- Travel support for the 2 lecturers and some participants.
- Travel support for some participants and accommodation for 4 participants.
- Other expenses.
We mention that two participants covered completely their own expenses.
Abstracts of the mini-courses
I. Geometric aspects of phase separation – Susanna Terracini (Università di Torino)
Several physical phenomena can be described by a certain number of densities (of mass, population, probability, …) distributed in a domain and subject to laws of diffusion, reaction, and competitive interaction. Whenever the competitive interaction is the prevailing phenomenon, the several densities can not coexist and tend to segregate, hence determining a partition of the domain (Gause’s experimental principle of competitive exclusion (1932)). As a model problem, we consider the system of stationary equations
\Delta u_i=f_i(u_i)-\beta u_i \sum_{j \neq i}g_{ij}(u_j) \qquad u_i>0\;
The cases g_{ij}(s)=\beta_{ij}s (Lotka-Volterra competitive interactions) and g_{ij}(s)=\beta_{ij}s^2 (gradient system for Gross-Pitaevskii energies) are of particular interest in the applications to population dynamics and theoretical physics respectively.
In this series of lectures, we will undertake the analysis of qualitative properties of solutions to systems of semilinear elliptic equations, whenever the parameter \beta , accounting for the competitive interactions, diverges to infinity. At the limit, when the minimal interspecific competition rate \beta=\min_{ij}{\beta_{ij}} diverges to infinity, we find a vector U=(u_1,\cdots,u_h) of functions with mutually disjoint supports: the segregated states: u_i\cdot u_j\equiv 0 , for i\neq j , satisfying
-\Delta u_i=f_i(x,u_i) \qquad {\rm whenever }\;u_i \neq 0\;, \ \ i=1,\ldots,h.
We will consider the following aspects:
- Spectral problems: optimal partitions w.r.t. eigenvalues in connection with monotonicity formulæ.
- Entire solutions of the competitive elliptic system:
-\Delta u_i = - \sum_{j \neq i} u_i u_j^2 \, \text{ in } \mathbb{R}^N, \qquad u_i >0 \, \text{ in }\mathbb{R}^N \qquad i=1,\dots,k.
- Competition-diffusion problems with fractional Laplacians.
- Competition-diffusion problems with nonlocal interactions.
- Spiralling solutions in the non symmetrical case.
II. An introduction to the fractional Yamabe problem – María del Mar González (Universidad Autónoma de Madrid)
The aim of this course is to present one very recent topic in differential geometry: the fractional Yamabe problem, both from the analytic and geometric points of view, but especially towards the PDE community interested in nonlocal problems.
The basic tool in conformal geometry is to understand the geometry of a space by studying the transformations on such space. The simplest differential operator with conformal properties is the conformal Laplacian L_h:= -\Delta_ h +\frac{n-2}{4(n-1)}R_h, and its associated curvature (which is precisely the scalar curvature R_h). It gives rise to interesting semilinear equations with reaction term of power type, such as the constant scalar curvature (or Yamabe) equation
- \Delta_h u + \frac{n-2}{4(n-1)}R_h = \frac{n-2}{4(n-1)} cu^{\frac{n+2}{n-2}}.
The Yamabe problem has been one of the multiple examples of the interaction between analysis and geometry.
A higher order example of a conformally covariant operator is the Paneitz operator, which is defined as the bi-Laplacian (-\Delta_h)^2 plus lower order curvature terms. Being M a Riemannian manifold with a Riemannian metric h, these operators belong to a general framework in which on the manifold (M, h) there exists a meromorphic family of conformally covariant pseudodifferential operators of fractional order
P^h_s= (-\Delta_h)^s + ... \quad \text{ for any } s \in(0, n/2).
P_h^s will be called the conformal fractional Laplacian. The main goal of this course is to describe and to give some examples, applications and open problems for this non-local object.
We will explain the construction of the conformal fractional Laplacian from a purely analytical point of view. Caffarelli and Silvestre gave a construction for the standard fractional Laplacian as a Dirichlet-to-Neumann operator of a uniformly degenerate elliptic boundary value problem. In the manifold case, Chang and the lecturer related the original definition of the conformal fractional Laplacian coming from scattering theory (in four-dimensional gravitational Physics) to a Dirichlet-to-Neumann operator for a related elliptic extension problem, thus allowing for an analytic treatment of Yamabe-type problems in the non-local setting.
Comments
The facilities of IML are awesome for this sort of events. The Institute is located in a very quiet area, close to a small village with basic facilities and well connected with Stockholm. The rooms and bunkers are lovely, very well-equipped. The new building with the seminar room is also nice; the shared kitchen next to the seminar room facilitates socialization and favors discussions in the nearby blackboard room. Of course, the main building—Mittag-Leffler’s former house—is simply amazing, and it definitively invites to retreat, study, reflection, work, and collaboration. We are also grateful to the administrative staff for their efficiency and support.

The participants of the Summer School, especially the junior ones, were happy to be given the opportunity to present their work. The relatively small size of the meeting ensured that they found themselves confident enough to discuss with each other.
Recent research topics in the field of Nonlocal Equations were presented by both experienced and young researchers. The social dinner and other communal activities ensured that the participants had the chance to get to know each other. A barbecue was organised on Tuesday. Wednesday afternoon was free several options for social activities were suggested (trips to the city center, a boat tour, visiting local museums).
Finally, the was a social dinner on Thursday, also supported by the Institut Mittag-Leffler itself.

Leave a Reply
You must be logged in to post a comment.